R ile kategorik veri
Kategorik veri hemen her yerde karşımıza çıkmakta ve bu verilerin analizi kendine has yöntemler gerektirmekte. İstatistik eğitiminde genellikle normal dağılıma sahip verilerin analizine ağırlık verilmesi ve bu analizlerin karmaşık boyutlara varabilmesi, kategorik veri analiz yöntemlerinin arka planda kalmasına sebebiyet verebilmekte. Bu notta R ile kategorik veri analizine değineceğim.
İkiye ayrılan yollar: Binomial dağılım
Her istatistiksel analiz model seçimiyle başlar. İstatistiksel model genellikle, veride gözlemlenen belirsizliği hesaplamamızı sağlayan bir olasılık dağılımı şeklidir. Bilindiği gibi kategorik değişkenlerde iki veya daha fazla kategori bulunabilir. En temel kategorik veri olan ikili (binary) bağımlı değişkene en uygun modele Bernoulli veya Binomial dağılımı adı verilir.
Mesela yeni geliştirilen bir ilacın hastalarda başarılı olup olmadığını gösteren Y değişkenini ele alırsak Y = 0 ilacın başarısız olduğu ve Y = 1 başarılı olduğunu ifade eder. Binomial dağılıma sahip bir değişkenin herhangi bir değerine ilişkin olasılığı şu formülle hesaplıyoruz: p(x) = choose(n, x) p^x (1-p)^(n-x). Binomial dağılım açısından önemli iki varsayım; denemelerin 1) birbirinin aynı olması ve 2) birbirlerinden bağımsız olmaları, yani bir denemenin sonucunun diğerlerini etkilememesidir.
dbinom() fonksiyonu bu formülü kullanarak söz konusu olasılığı hesaplamaktadır. Mesela yeni geliştirilen bir ilaç 10 hasta üzerinde test edilmek istendiğini ve ilacın başarı ihtimalinin de %40 olduğunu düşünelim. Bu durumda ilacın hastalardan beşi üzerinde başarılı olma ihtimalini şu şekilde hesaplayabiliriz:
dbinom(x = 5, size = 10, prob = 0.4)## [1] 0.2006581choose(10, 5) * 0.4^5 * (1-0.4)^(10-5)## [1] 0.20065815 kişinin iyileşmesi ihtimali %20. x parametresine dizi atamak suretiyle birden fazla ihtimali de hesaplayabiliriz. Şimdi bunu kullanarak olasılık değerlerinin bir grafiğini çizelim:
pmf <- data.frame(w = 0:10, prob = round(dbinom(x = 0:10, size = 10, prob = 0.4),3))
plot(x = pmf$w, y = pmf$prob, type = "h",
main = "", xlab = "Başarı", ylab = "Olasılık",
panel.first = grid(col = "gray", lty = "dotted"), lwd = 3)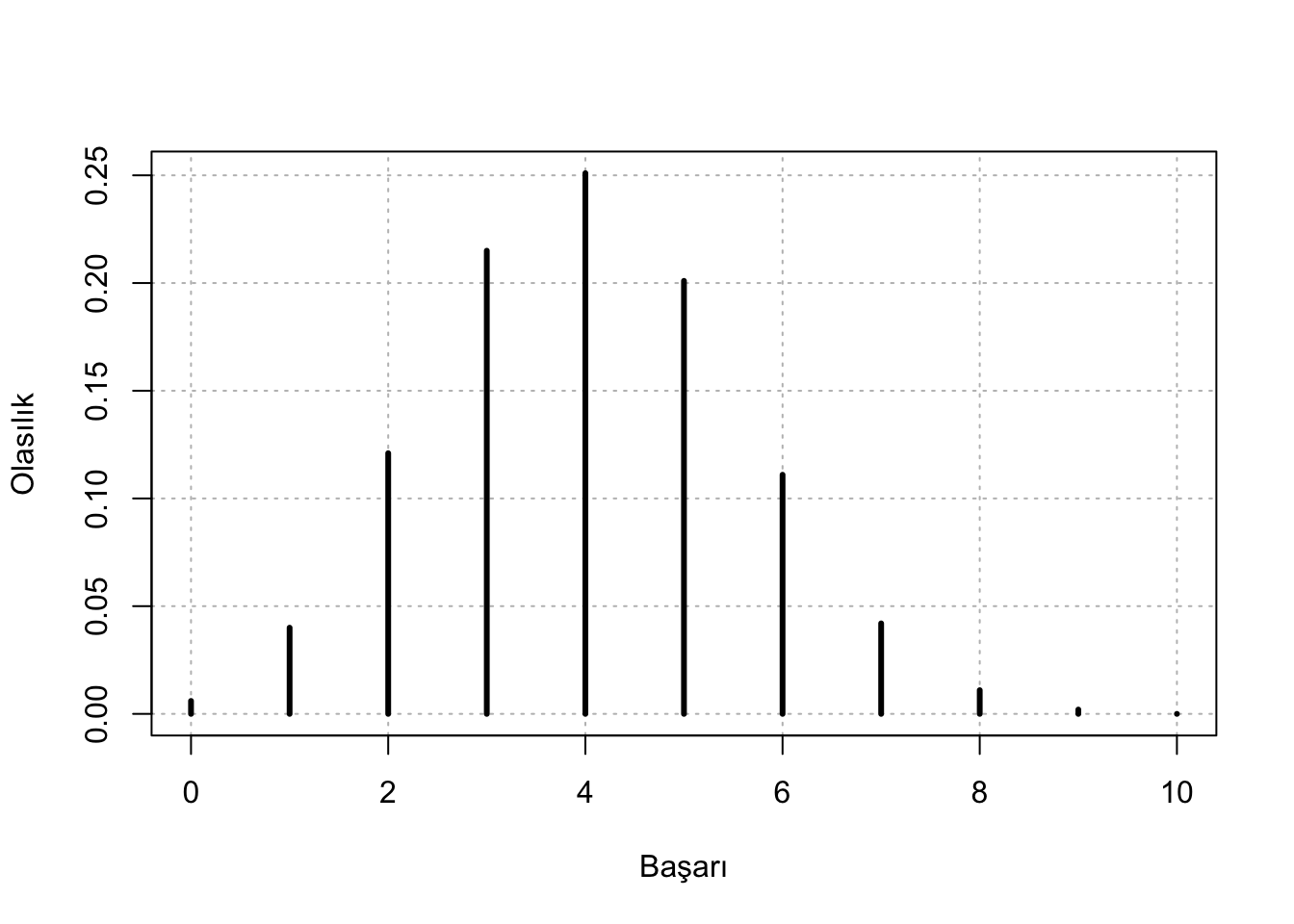
En yüksek ihtimal 4 başarı olması. dbinom() ile elde edeceğimiz olasılık değeri işe yarar olsa da özellikle akademik çalışmalarda güven aralığını unutmamak gerekir. Kategorik analizler için güven aralığını hesaplayan farklı yöntemler bulunmakta. Hepsinin artıları ve eksileri olduğundan eldeki veriye göre tercih yapılması gerekmekte. binom.test() ve prop.test() ile güven aralığını hesaplayabiliriz.
binom.test(5,10,.4)$conf.int## [1] 0.187086 0.812914
## attr(,"conf.level")
## [1] 0.95prop.test(5,10,.4)$conf.int## Warning in prop.test(5, 10, 0.4): Chi-squared approximation may be incorrect## [1] 0.201423 0.798577
## attr(,"conf.level")
## [1] 0.95binom.test() daha geniş bir aralık hesaplayan ve bazı kaynaklarda “kullanışsız” olarak nitelenen Clopper-Pearson yöntemini uygulamaktadır. prop.test() küçük örneklemlerde ve düşük olasılıklarda sağlıklı sonuç vermemekle eleştirilen Wilson CI kullanmaktadır. Yukarıdaki fonksiyonların güven aralığı (conf.int) dışındaki diğer parametrelerini yardım dosyasında bulabilirsiniz. exactci paketiyle farklı güven aralığı metodlarını kullanmak mümkün.
Her iki test de birer p değeri hesaplamakta. Kategorik veri için p değeri Wald, Score ve Likelihood-Ratio olmak üzere başlıca üç farklı metodla hesaplanabilmekte. Aralarında bazı nüanslar olmakla birlikte genel kullanım açısından çok fark taşımadığından olsa gerek ki R yardım dosyalarında yukarıdaki testlerde hangi yöntemin kullanıldığından bahsedilmemiş.
Bu kısmı kapatmadan önce rbinom() hakkında da bir örnek vermek istiyorum. Simulasyon hem analiz yaparken hem de istatistik eğitiminde önemli bir yöntem. Bütün istatistiksel yöntemlerin bir takım varsayımları bulunmakta. Simulasyonlar bu varsayımlar ihlal edildiğinde sonucun nasıl farklılaştığını anlamamıza yardımcı oluyor.
Yukarıdaki ilaç örneğine uygun 1000 gözlem içeren bir örneklem oluşturalım. Yani başarı oranı %40 olan yeni geliştirilen bir ilacı 1000 tane 10’ar kişilik gruplara uygulamamız halinde, her bir grupta meydana gelebilecek başarı sayılarını içeren bir örneklem simüle edelim:
set.seed(4554)
mcsim <- rbinom(n = 1000, size = 10, prob = 0.4)
table(mcsim) ## mcsim
## 0 1 2 3 4 5 6 7 8 9
## 8 50 125 211 263 185 108 32 16 2hist(mcsim, probability = TRUE, breaks = c(-0.5:10.5), main = "",
xlab = "Başarı", ylab = "Olasılık")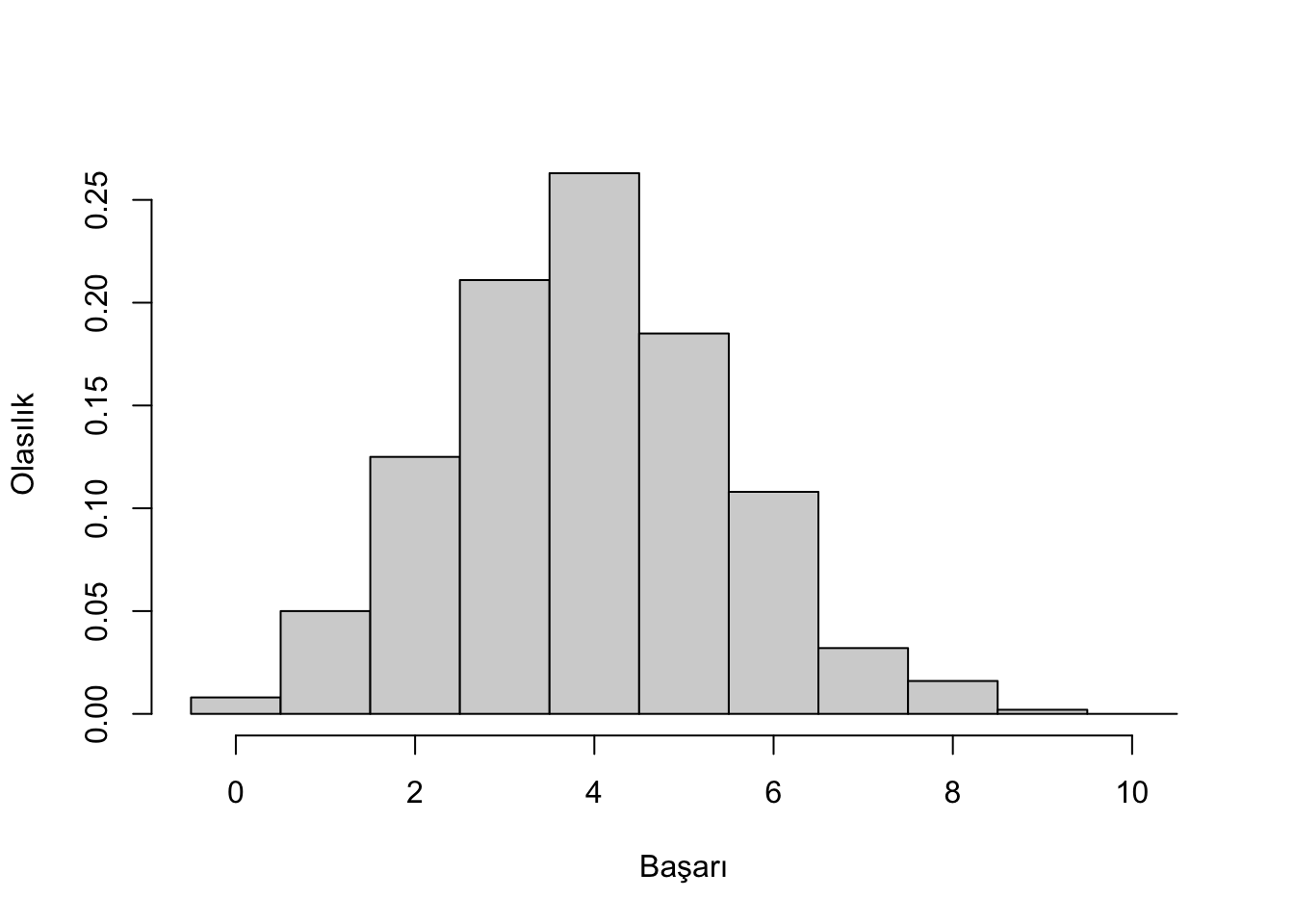
æ rastgele sayı üretme işleminde kullanılacak çekirdek değeri belirliyor. Çekirdek değer esasında bilgisayarca rastgele belirlenmekte. set.seed() ile bu değeri sabitleyerek simulasyon sonucunda sizde aynı değerleri elde etmiş oluyorsunuz.
2x2: İki Kategorili iki değişkenin hikayesi
Tek bir değişkenle ne kadar analiz olur? Pek fazla değil. Değişken sayısının artması analizin daha anlamlı olmasını sağlarken karmaşıklığı da illaki arttırmakta. Kategorik değişkenlerde bu karmaşıklığı daha fazla hissediyoruz. Biri bağımlı diğeri bağımsız iki binary değişken 2x2 ebatlarında bir tabloyla gösterilebilir. Hatırlarsanız bu tablolara kontenjans tablosu diyoruz. Kategori sayısı arttıkça tablodaki hücre sayısı artacaktır. Üçüncü bir değişken eklenmesi halinde tabloya bir boyut daha eklememiz gerekiyor.
Şimdi yukarıda bahsettiğimiz yeni ilacı test etmek için rastgele seçilen hastalara ilaç ve placebo verdiğimizi farz edelim. Hastaların iyileşme durumunu aşağıdaki gibi bir tabloyla ifade edebiliriz:
| Olumlu | Olumsuz | |
|---|---|---|
| İlaç | π1 | 1-π1 |
| Placebo | π2 | 1-π2 |
Yukarıda π olasılığı ifade etmektedir. Dolayısıyla tabloda ilk satır ilaç kullananlardan tedavisi başarılı ve başarısız olanların oranını, ikinci satır placebo kullananlardan tedavisi başarılı ve başarısız olanların oranını vermektedir. Bağımsız değişken ilaç veya placebo olmak üzere iki kategoriden oluşan tedavi değişkeni ve bağımlı değişken ilaçların olumlu veya olumsuz etkisini gösteren etki değişkeni.
Böyle bir tablonun analizinden muradımız öncelikle olasılıkları hesaplamak. Bunun için öncelikle veriyi array olarak kaydediyorum (veriler hayalidir):
t.table <- array(data = c(83, 67, 65, 101),
dim = c(2,2),
dimnames = list( c("ilaç", "placebo"), c("olumlu", "olumsuz")))
t.table## olumlu olumsuz
## ilaç 83 65
## placebo 67 101pi.t.table <- round(t.table/rowSums(t.table),3)
pi.t.table## olumlu olumsuz
## ilaç 0.561 0.439
## placebo 0.399 0.601Şayet elimizde yukarıdaki gibi sayılar değilde verisetinin kendisi varsa table() veya xtabs() fonksiyonlarından birisiyle yukarıdaki tabloları elde etmek mümkün:
dfTedavi <- data.frame(tedavi = rep(c("ilaç","placebo"), c(148,168)),
sonuc = rep(c("olumlu","olumsuz","olumlu","olumsuz"),c(83,65,67,101)))
table(dfTedavi)## sonuc
## tedavi olumlu olumsuz
## ilaç 83 65
## placebo 67 101İlaç ve placebo arasında istatistiksel olarak anlamlı bir fark olup olmadığını ölçmek için score test, Pearson chi-square test, ve likelihood ratio test (LRT)’den birisini kullanabiliriz. Score test ve Pearson chi-square test (üzerinde çalıştığımız örnekte) aynı sonucu verecektir Bunu prop.test() veya chisq.test() ile hesaplayabiliriz:
prop.test(x = t.table, conf.level = 0.95, correct = FALSE)##
## 2-sample test for equality of proportions without continuity
## correction
##
## data: t.table
## X-squared = 8.2812, df = 1, p-value = 0.004006
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## 0.05302749 0.27097509
## sample estimates:
## prop 1 prop 2
## 0.5608108 0.3988095chisq.test(x = t.table, correct = FALSE)##
## Pearson's Chi-squared test
##
## data: t.table
## X-squared = 8.2812, df = 1, p-value = 0.004006x olarak kontenjans tablosunu atadım, güven seviyesini %95 olarak ayarladım ve continuity correction yapılmasını istemedim. X2=8.281 ve p=0.004 değerleri ilaç ve placebo grupları arasında fark olmadığını savunan sıfır hipotezini reddedebileceğimizi göstermekte.
LRT içinse vcd paketinde yer alan assocstats() fonksiyonunu kullanabiliriz.
library(vcd)## Loading required package: gridassocstats(t.table)## X^2 df P(> X^2)
## Likelihood Ratio 8.3129 1 0.0039365
## Pearson 8.2812 1 0.0040057
##
## Phi-Coefficient : 0.162
## Contingency Coeff.: 0.16
## Cramer's V : 0.162Görüldüğü gibi LRT ile birlikte Pearson chi-square test sonucunu da aldık. Değerlerin birbirine yakın olması dikkate değer.
Yukarıdaki üç yöntem de olasılıklar arasındaki farkı ortaya koymaya yönelik, yani π1-π2. Haliyle sonuç örneklem büyüklüğünden etkilenmekte. Diğer yandan test sonucunun ve p değerininin yorumlanması ve anlaşılması her zaman sıkıntılı olmuştur. Bu yüzden gazete veya haber kanallarında anlaşılması daha kolay olan relative risk değeri sıkça rapor edilir. Relative risk π1/π2 şeklinde hesaplanır. Bizim örneğimizde relative risk 0.561/0.399 = 1.41 (olasılıkları yukarıda hesaplamıştık, pi.t.table değişkeni). Bunu ilaç kullanan hastaların tedavilerinin başarılı olma olasılığının placebo kullananlardan 1.41 kat daha fazla olduğu şeklinde yorumlayabiliriz.
Benzer bir istatistik de odds ratio. Daha çok bahislerde kullanılan bir terim. Mesela “A takımının kazanma şansı 1’e karşı 4” gibi bir kullanımı var. Odds ratio başarı olasılığının başarısızlık olasılığına veyahut birinci grubun olasılığının, ikinci grubun olasılığına oranlamasıyla bulunuyor. Dolayısıyla yorumlarken başarı/başarısızlık olarak değil de grupların taşıdığı anlamlara bakmak gerekiyor. Biz ilacın başarı ihtimalinden başladığımıdan yine aynı konuda devam edelim. Mesela bir ilacın başarı ihtimali %40 ise, odds ratio; 0.4/1-0.4=4/6=0.67. Yani ilaçla tedavinin başarı şansı 4’e karşı 6. Odds ratio bire eşit olması durumunda her iki durum aynı odds’a sahip. Birden büyük olması halinde birinci grup, küçük olması halinde ikinci grup daha fazla odds’a sahip. Yukarıdaki 2x2 tablomuz için odds ratio şu şekilde hesaplanır:
(OR <- t.table[1,1] * t.table[2,2] / (t.table[2,1] * t.table[1,2]))## [1] 1.924914Dolayısıyla tedavinin başarılı olma odds’u hastanın yeni ilaç kullanması durumunda 1.93 kat daha fazla olduğu anlaşılıyor.
Örneğimizde relative risk ve odds ratio tabiatıyla farklı sonuçlar veriyor. Şunu unutmamak gerek; odds ratio ihtimal ile aynı şey değil. Relative risk’i doğrudan “birinci grubun başarılı olma ihtimali ikinci grubun x katıdır” şeklinde yorumlamak mümkünken, odds ratio için bu tarz bir yorum yapılamaz. Odds ratio için “birinci grubun odds’u ikinci grubun x katıdır” diyebiliriz. Günlük hayatta pek kullanılmadığından ve anlaşılması da problemli olabildiğinden genellikle raporlarda relative risk kullanılmaktadır. Ancak odds ratio’nun istatistikte başka kullanım yerleri olduğundan ne olduğunu anlamak önemli.